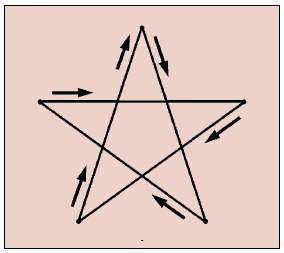
Знаете ли вы, что такое граф? Это такая наглядная геометрическая конструкция из точек (вершин) и соединяющих их линий (рёбер) вроде генеалогического древа или маршрута на карте. Некоторые графы можно нарисовать одним росчерком — не отрывая карандаша от бумаги и проходя по каждому ребру только один раз. Таким свойством обладает, например, граф в виде пятиконечной звезды. А чем он примечателен? Во-первых, этот граф связный: из любой вершины всегда можно перейти в другую по рёбрам. Во-вторых, из каждой вершины выходит чётное число рёбер.
Давно доказано, что всякий граф с такими свойствами можно нарисовать одним росчерком. При этом, начав движение из любой вершины, мы в итоге в неё же и вернёмся. А что будет, если отбросить последнее условие? Тогда можно допустить у графа наличие двух вершин, из которых выходит нечётное число рёбер. Ясно, что в этом случае обход фигуры следует начать из одной такой вершины, а закончить — в другой (например, одним росчерком на карте звёздного неба можно начертить ковш Большой Медведицы, соединив семь её наиболее ярких звёзд). Эти факты породили множество головоломок на вычерчивание замысловатых фигур. Одну из них придумал Кэрролл.
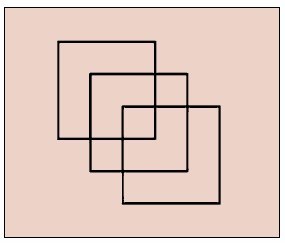
Взгляните на фигуру из трёх пересекающихся квадратов. Сможете ли вы нарисовать её, не отрывая карандаша от бумаги и не проводя более одного раза по каждой линии?